In what follows curly braces denote an optional argument. You should
note type them.
claim name {"tex_name"} formula.
Add the formula to the data-base as a theorem (claim) under the
given name.
You can give an optional TeX syntax (this TeX Syntax is used as in tex_syntax name "tex_name").
Cst syntax : sort.
Defines a constant of any sort.
>phox> Cst map : (nat -> nat) -> nat -> nat.
Constant added.
Default syntax is prefix. You can give a prefix, postfix
or infix syntax for instance the following
declarations allow the usual syntaxes for order 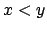 and factorial
and factorial
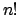 :
:
Cst Infix x "<" y : nat -> nat -> prop.
$< : d -> d -> prop
Cst Postfix[1.5] x "!" : nat -> nat.
$! : d -> d
To avoid too many parenthesis, you can also give a priority (a floating number) and, in case of infix notation, you can
precise if the symbol associates to the right (rInfix)
or to the left (lInfix).
For instance the following declarationsA.1
Cst Prefix[2] "S" x : nat -> nat.
Cst rInfix[3.5] x "+" y : nat -> nat -> nat.
Cst lInfix[3.5] x "-" y : nat -> nat -> nat.
Cst Infix[5] x "<" y : nat -> nat -> prop.
gives the following :
S x + y means (S x) + y
(parenthesis
around the expression with principal symbol of smaller weight) ;
x - y < x + y means (x - y) < (x + y)
(same reason) ;
x + y + z means x + (y + z) (right symbol first) ;
x - y - z means (x - y) - z (left symbol first).
More : the two symbols have the same priority and then x - y + z
is not a valid expression.
Arbitrary priorities are possible but can give a mess. You have ad least to
follows these conventions (used in the libraries) :
- connectives : priority
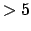 ;
;
- predicates : priority
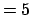 ;
;
- functions : priority
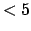 .
.
You can even define more complex syntaxes, for instance :
Cst Infix[4.5] x "==" y "mod" p : nat -> nat -> nat-> nat.
(* $== : nat -> nat -> nat -> nat *)
print \a,b(a + b == a mod b).
(* \a,b (a + b == a mod b) : nat -> nat -> nat *)
you can define syntax for binders :
Cst Prefix[4.9] "{" \P\ "in" a "/" P "}"
: 'a -> ('a -> prop) -> prop.
(* ${ : 'a -> ('a -> prop) -> prop *)
print \a \P{ x in a / P}.
(* \a,P {x in a / P } : ?a -> prop -> prop *)
{Local} def syntax = expression.
Defines an abbreviation using a given syntax for an expression.
The prefix Local tells that this definition should not be
exported. This means that if you use the Import or Use command,
only the exported definitions will be added.
Here are some examples :
>phox> def rInfix[7] X "&" Y = /\K ((X -> Y -> K) -> K).
(\X (\Y /\ K ((X -> Y -> K) -> K))) : Form -> Form -> Form
>phox> def rInfix[8] X "or" Y =
/\K ((X -> K) -> (Y -> K) -> K).
(\X (\Y /\ K ((X -> K) -> (Y -> K) -> K))) :
Form -> Form -> Form
>phox> def Infix [8.5] X "<->" Y = (X -> Y) & (Y -> X).
(\X (\Y (X -> Y) & (Y -> X))) : Form -> Form -> Form
>phox> def Prefix[5] "mu" \A\ \A\ A "<" t ">" =
/\X (/\x (A X x -> X x) -> X t).
(\A (\t /\ X (/\ x (A X x -> X x) -> X t))) :
((Term -> Form) -> Term -> Form) -> Term -> Form
Defintion of the syntax follows the same rules and conventions as for
the command Cst above.
{Local} def_thlist name = th1 ...thn.
Defines name to be the list of theorems th1 ...thn. For the moment list of theorems are useful only with commands
rewrite and rewrite_hyp.
>phox> def_thlist demorgan =
negation.demorgan disjunction.demorgan
forall.demorgan arrow.demorgan
exists.demorgan conjunction.demorgan.
del symbol.
Delete the given symbol from the data-base. All definitions,
theorems and rules using this symbol are deleted too.
>phox> del lesseq1.
delete lesseq_refl
delete inf_total from ##totality_axioms
delete inf_total
delete sup_total from ##totality_axioms
delete sup_total
delete less_total from ##totality_axioms
delete less_total
delete lesseq_total from ##totality_axioms
delete lesseq_total
delete lesseq1 from ##rewrite_rules
delete lesseq1
del_proof name.- Delete the proof of the given theorem (the theorem becomes a
claim).
Useful mainly to undo the
prove_claim command.
Sort {['a,'b, ...]} {= sort}.
Adds a new sort. The sort may have parameters or may be defined
from another sort.
>phox> Sort real.
Sort real defined
>phox> Sort tree['a].
Sort tree defined
>phox> Sort bool = prop.
Sort bool defined
For good understanding recall that the underlying proof system is
basically natural deduction, even if it is possible to add rules like
lefts rules of sequent calculus, see below.
{Local} close_def symbol.
When symbol is defined, this ``closes'' the definition. This
means that the definition can no more be open by usual proof commands
unless you explicitly ask it by using for instance proof commands unfold or unfold_hyp. In particular unification does not use
the definition anymore. This can in some case increase the efficiency
of the unification algorithm and the automatic tactic (or decrease if
not well used). When you have add enough properties and rules about a
given symbol with new_...commands, it can be a good thing to
``close'' it. Note that the first new_elim command closes the
definition for elimination rules, the first new_intro command
closes the definition for introduction rules. In case these two
commands are used, close_def ends it by closing the definition
for unification.
For (bad) implementation reasons the prefix Local is necessary in
case it is used for the definition of the symbol (see def
command). If not the definition will not be really local.
edel extension-list item.
Deletes the given item from the extension-list.
Possible extension lists are: rewrite (the list of rewriting
rules introduced by the new_equation command), elim, intro, (the introduction and elimination rules introduced by the
new_elim and new_intro {-t} commands), closed
(closed definitions introduced by the close_def command) and
tex (introduced by the tex_syntax command). The items can be names of theorems (new_...), or symbols ( close_def and tex_syntax). Use the eshow command for
listing extension lists.
>phox> edel elim All_rec.
delete All_rec from ##elim_ext
See also the del command.
elim_after_intro symbol.-
Warning: this command will disappear soon.
Tells the trivial tactic to try an elimination using an hypothesis starting
with the symbol constructor only if no introduction rule can be
applied on the current goal. (This seems to be useful only for the
negation).
>phox> def Prefix[6.3] "~" X = X -> False.
\X (X -> False) : Form -> Form
>phox> elim_after_intro $~.
Symbol added to "elim_after_intro" list.
{Local} new_elim {-i} {-n} {-t} symbol name { num} theorem.-
If the theorem has the following shape:
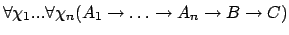 where symbol is the head of
where symbol is the head of 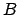 (the quantifier can be of any order
and intermixed with the implications if you wish). Then this theorem can be
added as an elimination rule for this symbol.
(the quantifier can be of any order
and intermixed with the implications if you wish). Then this theorem can be
added as an elimination rule for this symbol. 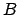 is the main
premise,
is the main
premise,
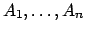 are the other premises and
are the other premises and 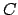 is the conclusion
of the rule.
is the conclusion
of the rule.
The name is used as an abbreviation when you want to precise which
rule to apply when using the elim command.
The optional num tells that the principal premise is the numth
premise whose head is symbol. The default is to take the first so this
is useful only when the first premise whose head is symbol is not the
principal one.
>phox> goal /\X /\Y (X & Y -> X).
|- /\ X,Y (X & Y -> X)
>phox> trivial.
proved
>phox> save and_elim_l.
Building proof .... Done.
Typing proof .... Done.
Verifying proof .... Done.
>phox> goal /\X /\Y (X & Y -> Y).
|- /\ X,Y (X & Y -> Y)
>>phox> trivial.
proved
>phox> save and_elim_r.
Building proof .... Done.
Typing proof .... Done.
Verifying proof .... Done.
>phox> new_elim $& l and_elim_l.
>phox> new_elim $& r and_elim_r.
If the leftmost proposition of the theorem is a propositional variable
(and then positively universally quantified), the rule defined by new_elim is called a left rule, that is like left rules of
sequent calculus.
The option [-i] tells the tactic trivial not to backtrack on such a
left rule. This option will be refused by the system if the theorem
donnot define a left rule. The option should be used for an invertible left rule, that is a rule that can commute with other
rules. A non sufficient condition is that premises of the rule are
equivalent to the conclusion.
A somewhat degenerate (there is no premises) case is :
>phox> proposition false.elim
/\X (False -> X).
trivial.
save.
%phox% 0 goal created.
proved
%phox% Building proof ....Done
Typing proof ....Done
Verifying proof ....Done
Saving proof ....Done
>phox> new_elim -i False n false.elim.
Theorem added to elimination rules.
The option [-n] tells the trivial tactic not to try to use this rule,
except if [-i] is also used. In this last case the two options [-i
-n] tell the tactic trivial to apply this rule first, and use it as
the left proof command, that is only once. Recall that in this
case the left rule should be invertible. For instance :
>phox> proposition conjunction.left
/\X,Y,Z ((Y -> Z -> X) -> Y & Z -> X).
trivial.
save.
>phox>
|- /\X,Y,Z ((Y -> Z -> X) -> Y & Z -> X)
%phox% 0 goal created.
proved
%phox% Building proof ....Done
Typing proof ....Done
Verifying proof ....Done
Saving proof ....Done
>phox> new_elim -n -i $& s conjunction.left.
Theorem added to elimination rules.
The option [-t] should be used for transitivity theorems. It gives
some optimisations for automatic tactics (subject to changes).
The prefix Local tells that this rule should not be exported. This
means that if you use the Import or Use command, only the
exported rules will be added.
You should also note that once one elimination rule has been
introduced, the symbol definition is no more expanded by the
elim tactic. The elim tactic only tries to apply each
elimination rule. Thus if a connective needs more that one
elimination rules, you should prove all the corresponding theorems and
then use the new_elim command.
new_equation {-l|-r|-b} name ....-
Add the given equations or conditional equations to the
equational reasoning used in conjunction with the high order
unification algorithm. name must be a claim or a theorem with
at least one equality as an atomic formula which is reachable from the
top of the formula by going under a universal quantifier or a
conjunction or to the right of an implication. This means that a
theorem like
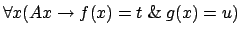 can be added
as a conditional equation. Moreover equations of the form
can be added
as a conditional equation. Moreover equations of the form 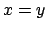 where
where 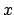 and
and 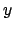 are variables are not allowed.
are variables are not allowed.
the option ``-l'' (the default) tells to use the equation from left to
right. The option ``-r'' tells to use the equation from right to left. The
option ``-b'' tells to use the equation in both direction.
>phox> claim add_O /\y:N (O + y = y).
>phox> claim add_S /\x,y:N (S x + y = S (x + y)).
>phox> new_requation add_O.
>phox> new_requation add_S.
>phox> goal /\x:N (x = O + x).
trivial.
>phox> proved
{Local} new_intro {-n} {-i} {-t} {-c} name theorem.-
If the theorem has the following shape:
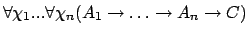 (the quantifier can be
of any order and intermixed with the implications if you wish), then
this theorem can be added as an introduction rule for
(the quantifier can be
of any order and intermixed with the implications if you wish), then
this theorem can be added as an introduction rule for symbol,
where symbol is the head of 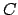 . The formulae
. The formulae
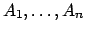 are the premises and
are the premises and  is the conclusion of the rule.
is the conclusion of the rule.
The name is used as an abbreviation when you want to precise which
rule to apply when using the intro command.
The option [-n] tells the trivial tactic not to try to use this rule.
The option [-i] tells the trivial tactic this rule is invertible. This
implies that the trivial tactic will not try other introduction rules
if an invertible one match the current goal, and will not backtrack on
these rules.
The option [-t] should be used when this rule is a totality theorem
for a function (like
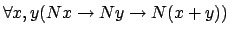 ), the
option [-c] for a totality theorem for a ``constructor'' like
), the
option [-c] for a totality theorem for a ``constructor'' like 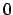 or
successor on natural numbers. It can give some optimisations on
automatic tactics (subject to changes). For the flag
or
successor on natural numbers. It can give some optimisations on
automatic tactics (subject to changes). For the flag auto_type to work properly we recommend to use the option [-i]
together with these two options (totality theorems are in general
invertible).
The prefix Local tells that this rule should not be exported. This
means that if you use the Import or Use command, only the
exported rules will be added.
You should also note that once one introduction rule has been
introduced, the symbol (head of  ) definition is no more
expanded by the
) definition is no more
expanded by the intro tactic. The intro tactic only tries to
apply each introduction rule. Thus if a connective has more that one
introduction rules, you should prove all the corresponding theorems
and then use the new_intro command.
>phox> goal /\X /\Y (X -> X or Y).
|- /\ X /\ Y (X -> X or Y)
>phox> trivial.
proved
>phox> save or_intro_l.
Building proof .... Done.
Typing proof .... Done.
Verifying proof .... Done.
>phox> goal /\X /\Y (Y -> X or Y).
|- /\ X /\ Y (Y -> X or Y)
>phox> trivial.
proved
>phox> save or_intro_r.
Building proof .... Done.
Typing proof .... Done.
Verifying proof .... Done.
>phox> new_intro l or_intro_l.
>phox> new_intro r or_intro_r.
add_path string.
Add string to the list of all path. This path list is used to find
files when using the Import, Use and include commands. You can set the
environment variable 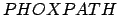 to set your own path (separating each
directory with a column).
to set your own path (separating each
directory with a column).
>phox> add_path "/users/raffalli/phox/examples".
/users/raffalli/phox/examples/
>phox> add_path "/users/raffalli/phox/work".
/users/raffalli/phox/work/
/users/raffalli/phox/examples/
Import module_name.
Loads the interface file ``module_name.afi'' (This file is produced by
compiling an file). Everything in this file is directly loaded, no
renaming applies and objects of the same name will be merged if this is
possible otherwise the command will fail.
A renaming applied to a module will not rename symbols added to the module
by the Import command (unless the renaming explicitly forces it).
Beware, if Import command fails when using interactively, the
file can be partially loaded which can be quite confusing !
include "filename".
Load an ASCII file as if all the characters in the file were typed
at the top-level.
Use {-n} module_name {renaming}.
Loads the interface file ``module_name.afi'' (This file is produced by
compiling a file). If given, the renaming is applied. Objects of
the same name (after renaming) will be merged if this is possible otherwise
the command will fail.
The option -n tells Use to check that the theory is not
extended. That is no new constant or axiom are added and no constant are
instantiated by a definition.
The syntax of renaming is the following:
renaming := renaming_sentence { |
renaming }
A renaming_sentence is one of the
following (the rule matching explicitly the longest part of the original
name applies):
name1 -> name2 : the symbol name1 is renamed to
named2.
_.suffix1 -> _.suffix2 : any symbol of the form xxx.suffix1 is renamed to xxx.suffix2 (a suffix can contain some
dots).
_.suffix1 -> _ : any symbol of the form xxx.suffix1 is renamed to xxx.
_ -> _.suffix2 : any symbol of the form xxx is renamed to xxx.suffix2.
from module_name with renaming. : symbols created
using the command Import module_name will be renamed using
the given renaming (By default they would not have been renamed).
A renaming applied to a module will rename symbols added to the module
by the Use command.
Beware, if Use command fails when using interactively, the
file can be partially imported which can be quite confusing !
depend theorem.- Gives the list of all axioms which have
been used to prove the
theorem.
>phox> depend add_total.
add_S
add_O
eshow extension-list.
Shows the given extension-list. Possible extension lists are
(See edel): equation (the list of equations
introduced by the new_equation command), elim, intro, (the introduction and elimination rules introduced by the
new_elim and new_intro {-t} commands), closed
(closed definitions introduced by the close_def command) and
tex (introduced by the tex_syntax command).
>phox> eshow elim.
All_rec
and_elim_l
and_elim_r
list_rec
nat_rec
flag name. or flag name value.
Prints the value (in the first form) or modify an internal flags of the
system. The different flags are listed in the index B.
>phox> flag axiom_does_matching.
axiom_does_matching = true
>phox> flag axiom_does_matching false.
axiom_does_matching = false
path.
Prints the list of all paths. This path list is used to find
files when using the include command.
>phox> path.
/users/raffalli/phox/work/
/users/raffalli/phox/examples/
print expression.- In case expression
is a closed expression of the language in use, prints it and gives its
sort, gives an (occasionally) informative error message otherwise. In
case expression is a defined expression (constant, theorem
...) gives the definition.
>PhoX> print \x,y (y+x).
\x,y (y + x) : nat -> nat -> nat
>PhoX> print \x (N x).
N : nat -> prop
>PhoX> print N.
N = \x /\X (X N0 -> /\y:X X (S y) -> X x) : nat -> prop
>PhoX> print equal.extensional.
equal.extensional = /\X,Y (/\x X x = Y x -> X = Y) : theorem
print_sort expression.- Similar to
print, but gives more information on sorts of bounded variable in
expressions.
>PhoX> print_sort \x,y:<nat (y+x).
\x:<nat,y:<nat (y + x) : nat -> nat -> nat
>PhoX> print_sort N.
N = \x:<nat /\X:<nat -> prop (X N0 -> /\y:<nat X (S y) -> X x)
: nat -> prop
priority list of symbols.- Print the priority of the given
symbols. If no symbol are
given, print the priority of all infix and prefix symbols.
>PhoX> priority N0 $S $+ $*.
S Prefix[2] nat -> nat
* rInfix[3] nat -> nat -> nat
+ rInfix[3.5] nat -> nat -> nat
N0 nat
search string type.
Prints the list of all symbols which have the type and whose name
contains the string. If no type is given, it prints all symbols
whose name contains the string. If the empty string is given, it prints
all symbols which have the type.
>PhoX> Import nat.
...
>PhoX> search "trans"
>PhoX> .
equal.transitive theorem
equivalence.transitive theorem
lesseq.ltrans.N theorem
lesseq.rtrans.N theorem
>PhoX> search "" nat -> nat -> prop.
!= Infix[5] 'a -> 'a -> prop
< Infix[5] nat -> nat -> prop
<= Infix[5] nat -> nat -> prop
<> Infix[5] nat -> nat -> prop
= Infix[5] 'a -> 'a -> prop
> Infix[5] nat -> nat -> prop
>= Infix[5] nat -> nat -> prop
predP nat -> nat -> prop
![]() and factorial
and factorial
![]() :
:
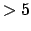 ;
;
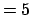 ;
;
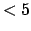 .
.